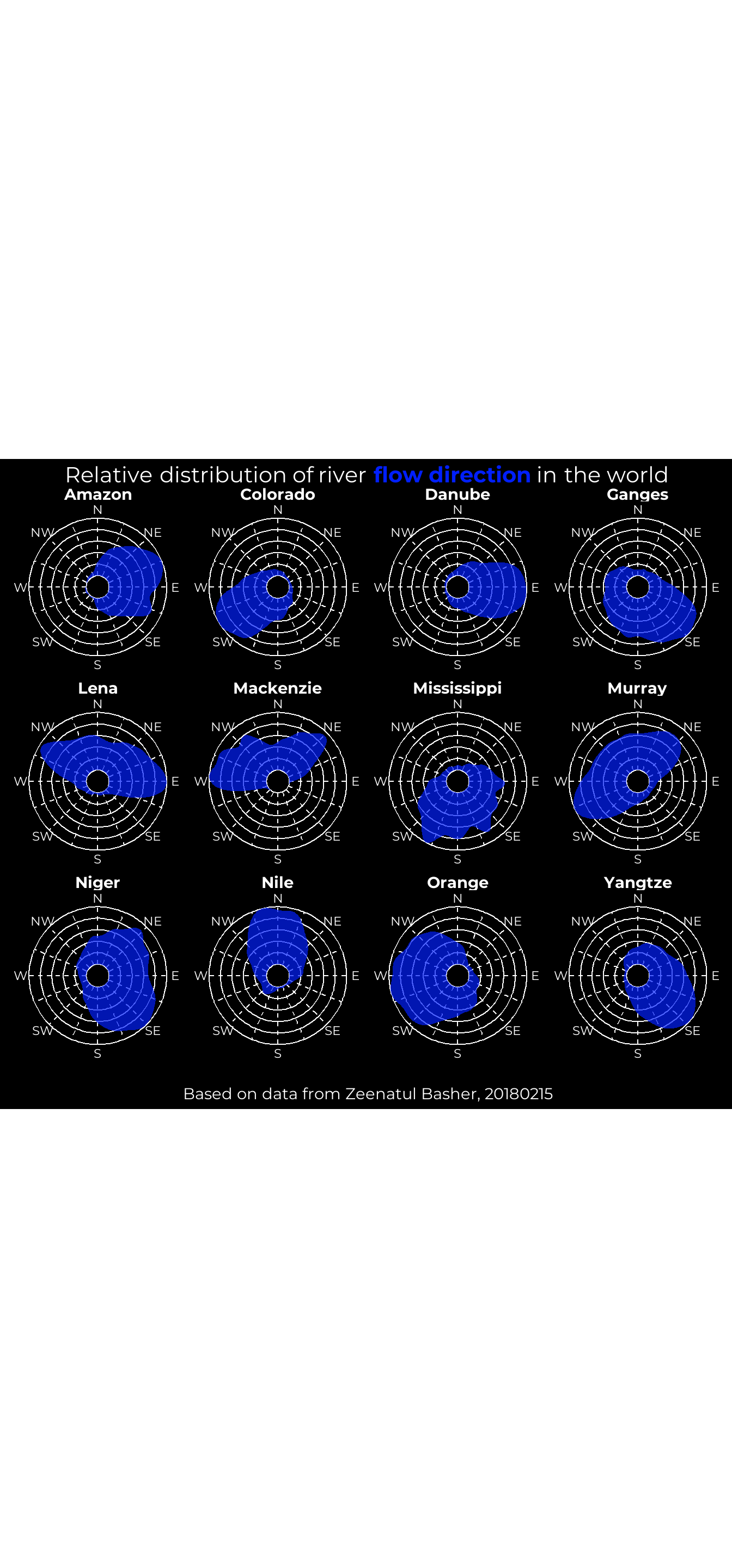
Direcciones del flujo fluvial
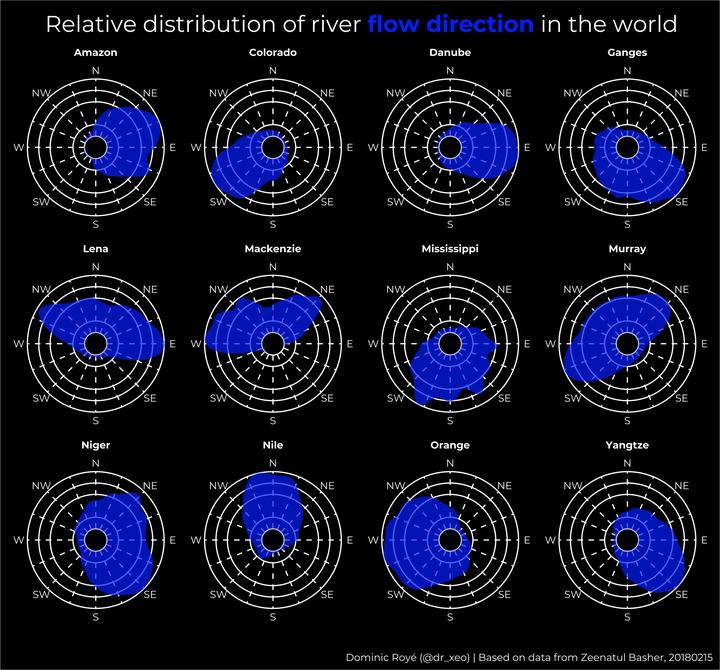
Recientemente creé una visualización de la distribución de las direcciones del flujo fluvial y también de las orientaciones costeras. A raíz de su publicación en los RRSS (aquí) me pidieron que hiciera un post acerca de cómo lo hice. Pues bien, aquí vamos para empezar con un ejemplo de los ríos, la orientación costera es algo más compleja. Lo mismo hice para una selección de ríos europeos aquí en este tweet. No obstante, originalmente empecé con la orientación de las costas europeas.
Have you ever wondered where the European #coasts are oriented? #rstats #ggplot2 #geography #dataviz pic.twitter.com/tpWVxSoHlw
— Dr. Dominic Royé (@dr_xeo) May 26, 2020
Paquetes
En este post usaremos los siguientes paquetes:
| Paquete | Descripción |
|---|---|
| tidyverse | Conjunto de paquetes (visualización y manipulación de datos): ggplot2, dplyr, purrr,etc. |
| remotes | Instalación desde repositorios remotos |
| qgisprocess | Interfaz entre R y QGIS |
| sf | Simple Feature: importar, exportar y manipular datos vectoriales |
| ggtext | Soporte para la representación de texto mejorado con ggplot2 |
| sysfonts | Cargar fuentes en R |
| showtext | Usar fuentes más fácilmente en gráficos R |
| circular | Funciones para trabajar con datos circulares |
| geosphere | Trigonometría esférica para aplicaciones geográficas |
En el caso del paquete qgisprocess es necesario instalar QIGS >= 3.16 aquí. Más adelante explicaré la razón del uso de QGIS.
# instalamos los paquetes si hace falta
if(!require("tidyverse")) install.packages("tidyverse")
if(!require("remotes")) install.packages("remotes")
if(!require("qgisprocess")) remotes::install_github("paleolimbot/qgisprocess")
if(!require("sf")) install.packages("sf")
if(!require("ggtext")) install.packages("ggtext")
if(!require("circular")) install.packages("circular")
if(!require("geosphere")) install.packages("geosphere")
if(!require("sysfonts")) install.packages("sysfonts")
if(!require("showtext")) install.packages("showtext")
# paquetes
library(sf)
library(tidyverse)
library(ggtext)
library(circular)
library(geosphere)
library(qgisprocess)
library(showtext)
library(sysfonts)Consideraciones iniciales
Los ángulos en líneas vectoriales se basan en el ángulo entre dos vértices, y el número de vértices depende de la complejidad, y en consecuencia de la resolución, de los datos vectoriales. Por tanto, puede haber diferencias en usar distintas resoluciones de una línea vectorial, sea de la costa o del río como en este ejemplo. Una línea recta simplemente se construye con dos puntos de longitud y latitud.
Relacionado con ello está la fractalidad, una estructura aparentemente irregular pero que se repite a diferentes escalas, de la línea de costa o también del río. La característica más paradójica es que la longitud de una línea costera depende de la escala de medida, cuanto menor es el incremento de medida, la longitud medida se incrementa.
Existen dos posibiliades de obtener los ángulos de los vértices. En la primera calculamos el ángulo entre todos los vértices consecutivos.
Por ejemplo, imaginémonos dos puntos, Madrid (-3.71, 40.43) y Barcelona (2.14, 41.4).
¿Cuál es el ángulo de su línea recta?
bearingRhumb(c(-3.71, 40.43), c(2.14, 41.4))## [1] 77.62391Vemos que es el de 77º, o sea, dirección noreste. Pero, ¿y si voy de Barcelona a Madrid?
bearingRhumb(c(2.14, 41.4), c(-3.71, 40.43))## [1] 257.6239El angúlo es diferente porque nos movemos desde el noreste al suroeste. Podemos invertir fácilmente el ángulo para obtener el movimiento contrario.
# ángulo contrario de Barcelona -> Madrid
bearingRhumb(c(2.14, 41.4), c(-3.71, 40.43)) - 180## [1] 77.62391# ángulo contrario de Madrid -> Barcelona
bearingRhumb(c(-3.71, 40.43), c(2.14, 41.4)) + 180## [1] 257.6239La dirección en la que calculamos los ángulos es importante. En el caso de los ríos se espera que sea la dirección de flujo de origen a la desembocadura, ahora bien, un problema puede ser que los vértices, que construyen las líneas, no estén ordenados geográficamente en la tabla de atributos. Otro problema puede ser que los vértices empiecen en la desembocadura lo que daría al angúlo inverso como lo hemos visto antes.
Sin embargo, hay una forma más fácil. Podemos aprovechar los atributos de los sistemas de coordenadas proyectados (proyección Robinson, etc) que incluyen el ángulo entre los vértices. Este último enfoque lo vamos usar en este post. Aún así, debemos prestar mucha atención a los resultados según lo dicho anteriormente.
Preparación
Datos
Descargamos las líneas centrales de los ríos más grandes del mundo (descarga), accesible también en Zeenatul Basher et al. 2018.
Importar y proyectar
Lo primero que hacemos es importar, proyectar y eliminar la tercera dimensión Z, usando el encadenamiento de las siguientes functions: st_read() nos ayuda a importar cualquier formato vectorial, st_zm() elimina la dimensión Z o M de una geometría vectorial y st_transform() proyecta los datos vectoriales a la nueva proyección en formato proj4. La combinación de las funciones la realizamos con el famoso pipe (%>%) que facilita la aplicación de una secuencia de funciones sobre un conjunto de datos, más detalles en este post. Todas las funciones del paquete sf comienzan por st_* haciendo referencia al carácter espacial de su aplicación, similar a PostGIS. Igualmente, y al mismo estilo que PostGIS, se usan verbos como nombres de función.
proj_rob <- "+proj=robin +lon_0=0 +x_0=0 +y_0=0 +ellps=WGS84 +datum=WGS84 +units=m no_defs"
river_line <- st_read("RiverHRCenterlinesCombo.shp") %>%
st_zm() %>%
st_transform(proj_rob)## Reading layer `RiverHRCenterlinesCombo' from data source
## `E:\GitHub\blog_update_2021\content\es\post\2020-07-24-direcciones-del-flujo-fluvial\RiverHRCenterlinesCombo.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 78 features and 6 fields
## Geometry type: MULTILINESTRING
## Dimension: XYZ
## Bounding box: xmin: -164.7059 ymin: -36.97094 xmax: 151.5931 ymax: 72.64474
## z_range: zmin: 0 zmax: 0
## Geodetic CRS: WGS 84Extraer los ángulos
En el siguiente paso debemos extraer los ángulos de los vértices. Desgraciadamente, hasta donde sepa, no es posible extraer los atributos con alguna función del paquete sf. Aunque la función st_coordinates() nos devuelve las coordenadas, no incluye otros atributos. Por eso, debemos usar otra forma, y es que el open software Quantum GIS extrae todos los atributos de los vértices. Podríamos importar los datos vectoriales en QGIS Desktop y exportar los vértices desde allí, pero también es posible acceder a las funciones de QGIS desde R directamente.
Para ello, tenemos que tener instalado QGIS en OSGeo4W. El paquete qgisprocess nos permite de forma muy fácil usar las funciones del programa en R. Primero empleamos la función qgis_configure() para definir todas las rutas necesarias de QGIS.
# rutas a QGIS
qgis_configure()## getOption('qgisprocess.path') was not found.## Sys.getenv('R_QGISPROCESS_PATH') was not found.## Trying 'qgis_process' on PATH## Error in processx::run("cmd.exe", c("/c", "call", path, args), ...): System command 'cmd.exe' failed, exit status: 1, stderr:
## E> "qgis_process" no se reconoce como un comando interno o externo,
## E> programa o archivo por lotes ejecutable.## Found 1 QGIS installation containing 'qgis_process':
## C:/Program Files/QGIS 3.18/bin/qgis_process-qgis.bat## Trying command 'C:/Program Files/QGIS 3.18/bin/qgis_process-qgis.bat'## Success!## QGIS version: 3.18.1-Zürich## Metadata of 986 algorithms queried and stored in cache.
## Run `qgis_algorithms()` to see them.La función qgis_algorithms() nos ayuda a buscar diferentes herramientas de QGIS. Además la función qgis_show_help() especifica la forma de uso con todos los argumentos requeridos.
# buscar herramientas
qgis_algorithms()## # A tibble: 986 x 5
## provider provider_title algorithm algorithm_id algorithm_title
## <chr> <chr> <chr> <chr> <chr>
## 1 3d QGIS (3D) 3d:tessellate tessellate Tessellate
## 2 gdal GDAL gdal:aspect aspect Aspect
## 3 gdal GDAL gdal:assignprojection assignproje~ Assign project~
## 4 gdal GDAL gdal:buffervectors buffervecto~ Buffer vectors
## 5 gdal GDAL gdal:buildvirtualraster buildvirtua~ Build virtual ~
## 6 gdal GDAL gdal:buildvirtualvector buildvirtua~ Build virtual ~
## 7 gdal GDAL gdal:cliprasterbyextent cliprasterb~ Clip raster by~
## 8 gdal GDAL gdal:cliprasterbymaskla~ cliprasterb~ Clip raster by~
## 9 gdal GDAL gdal:clipvectorbyextent clipvectorb~ Clip vector by~
## 10 gdal GDAL gdal:clipvectorbypolygon clipvectorb~ Clip vector by~
## # ... with 976 more rows# uso de la herramienta
qgis_show_help("native:extractvertices")## Extract vertices (native:extractvertices)
##
## ----------------
## Description
## ----------------
## This algorithm takes a line or polygon layer and generates a point layer with points representing the vertices in the input lines or polygons. The attributes associated to each point are the same ones associated to the line or polygon that the point belongs to.
##
## Additional fields are added to the point indicating the vertex index (beginning at 0), the vertex’s part and its index within the part (as well as its ring for polygons), distance along original geometry and bisector angle of vertex for original geometry.
##
## ----------------
## Arguments
## ----------------
##
## INPUT: Input layer
## Argument type: source
## Acceptable values:
## - Path to a vector layer
## OUTPUT: Vertices
## Argument type: sink
## Acceptable values:
## - Path for new vector layer
##
## ----------------
## Outputs
## ----------------
##
## OUTPUT: <outputVector>
## VerticesEn nuestro caso la herramienta para extraer los vértices es simple y sólo lleva una entrada y una salida. La función qgis_run_algorithm()() ejecuta una herramienta de QGIS indicando el algoritmo y sus argumentos. La ventaja de usar el algoritmo directamente desde R es que podemos pasar objetos de clase sf (o sp) y raster que tenemos importados o creados en R. Como salida creamos un geojson, también podría ser de otro formato vectorial, y lo guardamos en una carpeta temporal. Para obtener el resultado de QGIS sólo necesitamos emplear la función qgis_output().
river_vertices <- qgis_run_algorithm(alg = "native:extractvertices",
INPUT = river_line,
OUTPUT = file.path(tempdir(), "rivers_world_vertices.geojson"))## Running cmd.exe /c call \
## "C:/Program Files/QGIS 3.18/bin/qgis_process-qgis.bat" run \
## "native:extractvertices" \
## "--INPUT=C:\Users\xeo19\AppData\Local\Temp\RtmpIns79r\file67a81d8f1f66\file67a840795857.gpkg" \
## "--OUTPUT=C:\Users\xeo19\AppData\Local\Temp\RtmpIns79r/rivers_world_vertices.geojson"
##
## ----------------
## Inputs
## ----------------
##
## INPUT: C:\Users\xeo19\AppData\Local\Temp\RtmpIns79r\file67a81d8f1f66\file67a840795857.gpkg
## OUTPUT: C:\Users\xeo19\AppData\Local\Temp\RtmpIns79r/rivers_world_vertices.geojson
##
##
## 0...10...20...30...40...50...60...70...80...90...
## ----------------
## Results
## ----------------
##
## OUTPUT: C:\Users\xeo19\AppData\Local\Temp\RtmpIns79r/rivers_world_vertices.geojsonriver_vertices <- st_read(qgis_output(river_vertices, "OUTPUT"))## Reading layer `rivers_world_vertices' from data source
## `C:\Users\xeo19\AppData\Local\Temp\RtmpIns79r\rivers_world_vertices.geojson'
## using driver `GeoJSON'
## Simple feature collection with 339734 features and 12 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -12117400 ymin: -3953778 xmax: 13751910 ymax: 7507359
## Geodetic CRS: WGS 84river_vertices no debes preocuparte.
Selección
Antes de seguir con la estimación de la distribución de los ángulos, filtramos algunos ríos de interés. Las funciones de la colección tidyverse son compatibles con el paquete sf. En el último post hice una introducción a tidyverse aquí.
river_vertices <- filter(river_vertices,
NAME %in% c("Mississippi", "Colorado",
"Amazon", "Nile", "Orange",
"Ganges", "Yangtze", "Danube",
"Mackenzie", "Lena", "Murray",
"Niger")
)
river_vertices ## Simple feature collection with 94702 features and 12 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -10377520 ymin: -3953778 xmax: 13124340 ymax: 7507359
## Geodetic CRS: WGS 84
## First 10 features:
## fid NAME SYSTEM name_alt scalerank rivernum Length_km vertex_index
## 1 6 Nile <NA> <NA> 1 4 3343.871 0
## 2 6 Nile <NA> <NA> 1 4 3343.871 1
## 3 6 Nile <NA> <NA> 1 4 3343.871 2
## 4 6 Nile <NA> <NA> 1 4 3343.871 3
## 5 6 Nile <NA> <NA> 1 4 3343.871 4
## 6 6 Nile <NA> <NA> 1 4 3343.871 5
## 7 6 Nile <NA> <NA> 1 4 3343.871 6
## 8 6 Nile <NA> <NA> 1 4 3343.871 7
## 9 6 Nile <NA> <NA> 1 4 3343.871 8
## 10 6 Nile <NA> <NA> 1 4 3343.871 9
## vertex_part vertex_part_index distance angle geometry
## 1 0 0 0.000 31.096005 POINT (3037149 1672482)
## 2 0 1 1208.130 22.456672 POINT (3037772 1673517)
## 3 0 2 2324.160 8.602259 POINT (3038039 1674600)
## 4 0 3 3656.452 8.573580 POINT (3038118 1675930)
## 5 0 4 5735.538 24.406889 POINT (3038612 1677950)
## 6 0 5 6758.322 25.134763 POINT (3039200 1678787)
## 7 0 6 10432.834 6.998982 POINT (3040164 1682333)
## 8 0 7 14865.136 4.239641 POINT (3040070 1686764)
## 9 0 8 16563.207 358.730530 POINT (3040356 1688438)
## 10 0 9 18376.526 347.480822 POINT (3039972 1690210)Estimar la distribución
Para visualizar la distribución podemos usar, o bien un histograma o un gráfico de densidad. Pero en el caso de estimar la función de densidad de probabilidad nos encontramos con un problema matemático a la hora de aplicarlo a datos circulares. No debemos usar la función estandar de R density() dado que en nuestros datos una dirección de 360º es la misma a 0º, lo que provocaría errores en este rango de valores. Es un problema general para diferentes métricas estadísticas. Más detalles estadísticos se explican en el paquete circular. Este paquete permite definir las características de los datos circulares (unidad, tipo de datos, rotación, etc.) como una clase de objeto en R.
Por tanto, lo que hacemos es construir una función que estime la densidad y devuelva una tabla con los ángulos (x) y las estimaciones de densidad (y). Dado que los ríos tienen diferentes longitudes, y queremos ver diferencias independientemente de ello, normalizamos las estimaciones usando el valor máximo. A diferencia de la función density(), en la que el ancho de banda de suavizado bw es optimizado, aquí es requerido indicarlo. Es similar a definir el ancho de barra en un histograma. Existe una función de optimización para la banda, bw.nrd.circular() que se podría emplear aquí.
dens_circ <- function(x){
dens <- density.circular(circular(x$angle, units = "degrees"),
bw = 70, kernel = "vonmises",
control.circular = list(units = "degrees"))
df <- data.frame(x = dens$x, y = dens$y/max(dens$y))
return(df)
}Para finalizar, estimamos la densidad de cada río de nuestra selección. Empleamos la función split() de R Base para obtener una tabla de cada río en una lista. Después aplicamos con la función map_df() del paquete purrr nuestra función de estimación de densidad a la lista. El sufijo _df permite que obtengamos una tabla unida, en lugar de una lista con los resultados de cada río. No obstante, es necesario indicar el nombre de la columna con el argumento .id, la que contendrá el nombre de cada río. En caso contrario no sabríamos diferenciar los resultados. También aquí recomiendo leer más detalles en el último post sobre tidyverse aquí.
dens_river <- split(river_vertices, river_vertices$NAME) %>%
map_df(dens_circ, .id = "river")
# resultado
head(dens_river)## river x y
## 1 Amazon 0.000000 0.2399907
## 2 Amazon 0.704501 0.2492548
## 3 Amazon 1.409002 0.2585758
## 4 Amazon 2.113503 0.2679779
## 5 Amazon 2.818004 0.2774859
## 6 Amazon 3.522505 0.2871232Visualización
Ahora ya sólo nos queda la visualización mediante el famoso paquete ggplot. Primero añadimos una nueva fuente Montserrat para usarla en este gráfico.
# descarga de fuente
font_add_google("Montserrat", "Montserrat")
# usar showtext para fuentes
showtext_opts(dpi = 200)
showtext_auto() En el siguiente paso creamos dos objetos con el título y con una nota de pie. En el título estamos usando un código html para dar color a una parte de texto en sustitución de una leyenda. Se puede usar html de forma muy fácil con el paquete ggtext.
# título con html
title <- "Relative distribution of river <span style='color:#011FFD;'><strong>flow direction</strong></span> in the world"
caption <- "Based on data from Zeenatul Basher, 20180215"La cuadrícula de fondo que crea ggplot por defecto para coordenadas polares no me convenció, por eso creamos una tabla con las líneas de fondo del eje x.
grid_x <- tibble(x = seq(0, 360 - 22.5, by = 22.5),
y = rep(0, 16),
xend = seq(0, 360 - 22.5, by = 22.5),
yend = rep(Inf, 16))A continuación definimos todos los estilos del gráfico. Lo más importante en este paso es la función element_textbox() del paquete ggtext para poder interpretar nuestro código html incorporado al título.
theme_polar <- function(){
theme_minimal() %+replace%
theme(axis.title.y = element_blank(),
axis.text.y = element_blank(),
legend.title = element_blank(),
plot.title = element_textbox(family = "Montserrat",
hjust = 0.5,
colour = "white",
size = 15),
plot.caption = element_text(family = "Montserrat",
colour = "white"),
axis.text.x = element_text(family = "Montserrat",
colour = "white"),
strip.text = element_text(family = "Montserrat",
colour = "white",
face = "bold"),
panel.background = element_rect(fill = "black"),
plot.background = element_rect(fill = "black"),
panel.grid = element_blank()
)
}Para terminar construimos el gráfico: 1) Usamos la función geom_hline() con diferentes puntos de intersección en y para crear la cuadrícula de fondo. La función geom_segment() crea la cuadrícula en x. 2) El área de densidad la creamos usando la función geom_area(). 3) En scale_x_continous() definimos un límite inferior
negativo para que no colapse en un punto pequeño. Las etiquetas de las ocho direcciones principales las indicamos en la función scale_y_continous(), y 4) Por último, cambiamos a un sistema de coordenadas polar y fijamos la variable para crear facetas.
ggplot() +
geom_hline(yintercept = c(0, .2, .4, .6, .8, 1), colour = "white") +
geom_segment(data = grid_x ,
aes(x = x, y = y, xend = xend, yend = yend),
linetype = "dashed", col = "white") +
geom_area(data = dens_river,
aes(x = x, y = y, ymin = 0, ymax = y),
alpha = .7,
colour = NA,
show.legend = FALSE,
fill = "#011FFD") +
scale_y_continuous(limits = c(-.2, 1), expand = c(0, 0)) +
scale_x_continuous(limits = c(0, 360),
breaks = seq(0, 360 - 22.5, by = 22.5),
minor_breaks = NULL,
labels = c("N", "", "NE", "", "E", "", "SE", "",
"S", "", "SW", "", "W", "", "NW", "")) +
coord_polar() +
facet_wrap(river ~ ., ncol = 4) +
labs(title = title, caption = caption, x = "") +
theme_polar()## Warning: Ignoring unknown aesthetics: ymin, ymax