Calcular la distancia al mar en R
En geografía, la distancia al mar es una variable fundamental, especialmente relevante a la hora de modelizar. Por ejemplo, en interpolaciones de la temperatura del aire habitualmente se hace uso de la distancia al mar como variable predictora, ya que existe una relación casual entre ambas que explica la variación espacial. ¿Cómo podemos estimar la distancia (más corta) a la costa en R?
Paquetes
En este post usaremos los siguientes paquetes:
| Paquete | Descripción |
|---|---|
| tidyverse | Conjunto de librerías (visualización y manipulación de datos): ggplot2, dplyr, etc. |
| sf | Simple Feature: importar, exportar y manipular datos vectoriales |
| raster | Importar, exportar y manipular raster |
| rnaturalearth | Conjunto de mapas vectoriales ‘natural earth’ |
| RColorBrewer | Paletas de colores |
#instalamos los paquetes si hace falta
if(!require("tidyverse")) install.packages("tidyverse")
if(!require("sf")) install.packages("sf")
if(!require("raster")) install.packages("raster")
if(!require("rnaturalearth")) install.packages("rnaturalearth")
#paquetes
library(rnaturalearth)
library(sf)
library(raster)
library(tidyverse)
library(RColorBrewer)La costa de Islandia como ejemplo
Nuestro ejemplo en este post será Islandia, como es un territorio insular facilitará el ensayo y de este modo es posible mostrar el proceso de forma sencilla. La librería rnaturalearth permite importar los límites de países (con diferentes niveles administrativos) de todo el mundo. Los datos vienen de la plataforma naturalearthdata.com. Recomiendo explorar la librería, más info aquí. La función ne_countries( ) importa los límites de países. En este caso indicamos con el argumento scale la resolución (10,50 o 110m), con country indicamos el país concreto de interés y con returnclass determinamos que clase queremos (sf o sp), en nuestro caso sf (simple feature).
world <- ne_countries(scale = 50) #mapamundi con 50m de resolución
plot(world) #tiene clase sp por defecto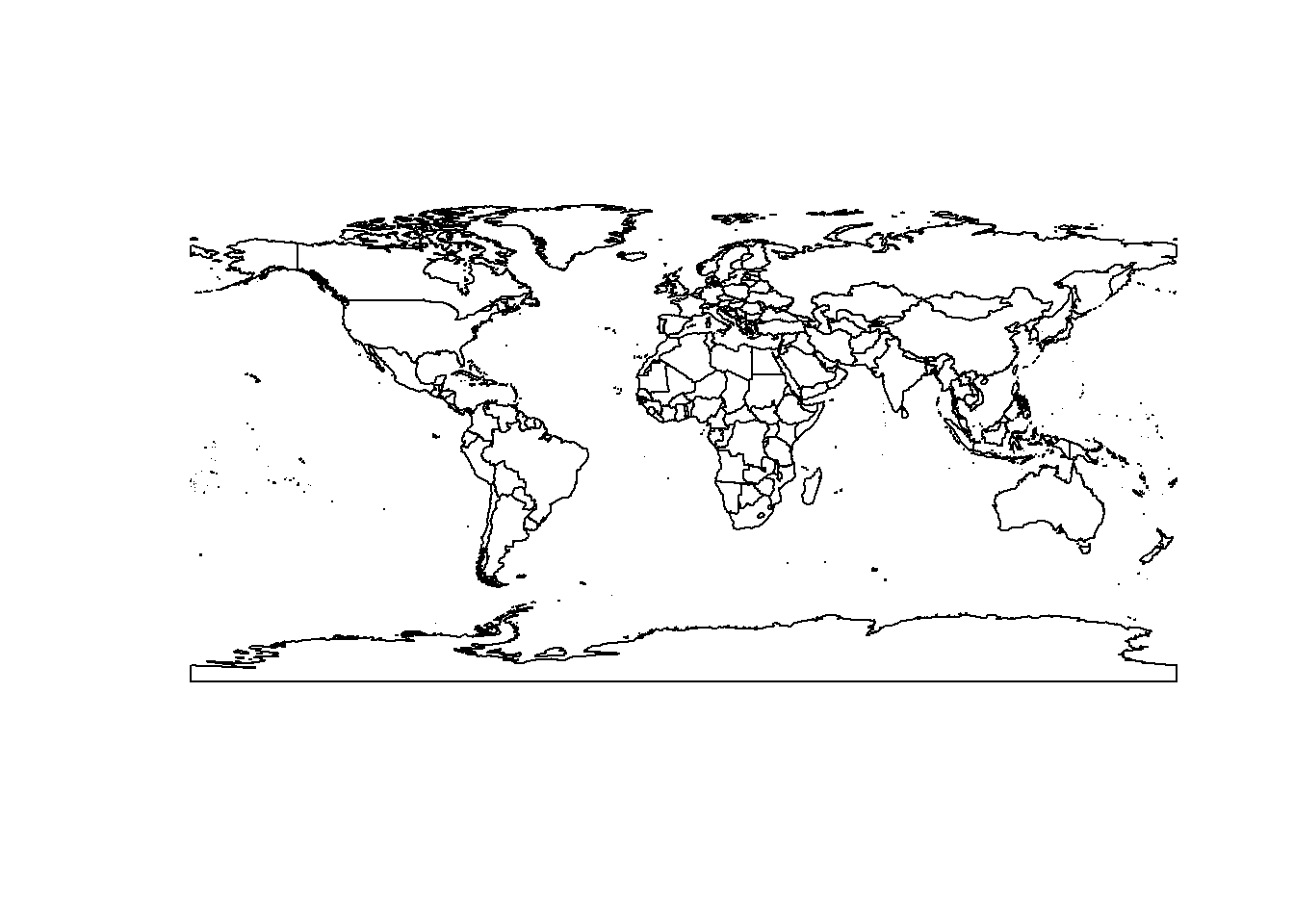
#importamos los límites de Islandia
iceland <- ne_countries(scale = 10,country = "Iceland", returnclass = "sf")
#info del objeto vectorial
iceland## Simple feature collection with 1 feature and 94 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -24.53991 ymin: 63.39671 xmax: -13.50292 ymax: 66.56415
## CRS: +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0
## featurecla scalerank labelrank sovereignt sov_a3 adm0_dif level
## 188 Admin-0 country 0 3 Iceland ISL 0 2
## type admin adm0_a3 geou_dif geounit gu_a3 su_dif subunit
## 188 Sovereign country Iceland ISL 0 Iceland ISL 0 Iceland
## su_a3 brk_diff name name_long brk_a3 brk_name brk_group abbrev postal
## 188 ISL 0 Iceland Iceland ISL Iceland <NA> Iceland IS
## formal_en formal_fr name_ciawf note_adm0 note_brk name_sort
## 188 Republic of Iceland <NA> Iceland <NA> <NA> Iceland
## name_alt mapcolor7 mapcolor8 mapcolor9 mapcolor13 pop_est pop_rank
## 188 <NA> 1 4 4 9 339747 10
## gdp_md_est pop_year lastcensus gdp_year economy
## 188 16150 2017 NA 2016 2. Developed region: nonG7
## income_grp wikipedia fips_10_ iso_a2 iso_a3 iso_a3_eh iso_n3
## 188 1. High income: OECD NA IC IS ISL ISL 352
## un_a3 wb_a2 wb_a3 woe_id woe_id_eh woe_note adm0_a3_is
## 188 352 IS ISL 23424845 23424845 Exact WOE match as country ISL
## adm0_a3_us adm0_a3_un adm0_a3_wb continent region_un subregion
## 188 ISL NA NA Europe Europe Northern Europe
## region_wb name_len long_len abbrev_len tiny homepart min_zoom
## 188 Europe & Central Asia 7 7 7 NA 1 0
## min_label max_label ne_id wikidataid name_ar name_bn name_de name_en
## 188 2 7 1159320917 Q189 <NA> <NA> Island Iceland
## name_es name_fr name_el name_hi name_hu name_id name_it name_ja name_ko
## 188 Islandia Islande <NA> <NA> Izland Islandia Islanda <NA> <NA>
## name_nl name_pl name_pt name_ru name_sv name_tr name_vi name_zh
## 188 IJsland Islandia Islândia <NA> Island Izlanda Iceland <NA>
## geometry
## 188 MULTIPOLYGON (((-14.56363 6...#aquí Islandia
plot(iceland)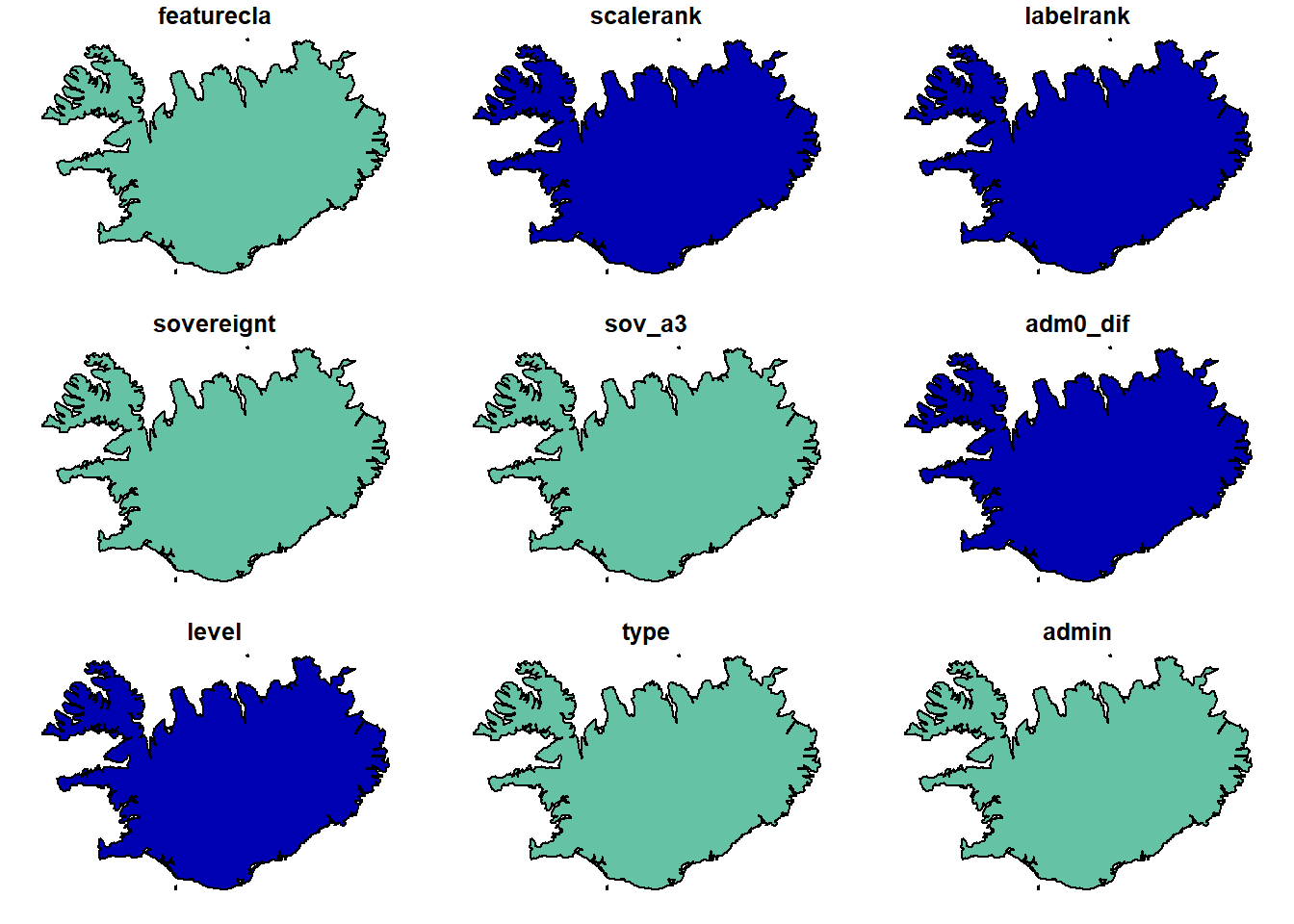
Por defecto, la función plot( ) con la clase sf nos crea tantas facetas del mapa como variables tiene. Para limitarlo podemos usar o bien con el nombre de una variable plot(iceland["admin"]) o el argumento max.plot plot(iceland,max.plot=1). Con el argumento max.plot=1 la función usa la primera variable disponible del mapa.
Además, vemos en la información del objeto sf que la proyección es WGS84 con grados decimales (código EPSG:4326). Para el cálculo de distancias es más conveniente usar metros en lugar de grados. Debido a ello, lo primero que hacemos es transformar el mapa de Islandia a UTM Zona 27 (código EPSG:3055). Más información sobre EPSG y proyecciones aquí. Con ese objetivo, usamos la función st_transform( ). Simplemente indicamos el mapa y el código EPSG.
#transformamos a UTM
iceland <- st_transform(iceland, 3055)Crear una red de puntos
Todavía necesitamos los puntos donde queremos conocer la distancia. En nuestro caso será una red regular de puntos en Islandia con una resolución de 5km. Esa tarea la hacemos con la función st_make_grid( ), indicando con el argumento cellsize la resolución en la unidad del sistema de coordenadas (metros en nuestro caso) y qué geometría nos gustaría crear what (poligonos, centros o esquinas).
#crear red de puntos
grid <- st_make_grid(iceland,cellsize = 5000, what = "centers")
#nuestra red sobre la extensión de Islandia
plot(grid)
#exraemos sólamente los puntos en los límites de Islandia
grid <- st_intersection(grid, iceland)
#nuestra red ahora
plot(grid)
Calcular la distancia
Para estimar la distancia usamos la función st_distance( ) que nos devuelve un vector de distancias para todos nuestros puntos de la red. Pero antes es necesario transformar el mapa de Islandia de una forma de polígono (MULTIPOLYGON) a línea (MULTILINESTRING). Más detalles con ?st_cast.
#convertimos Islandia de geometría poligono a línea
iceland <- st_cast(iceland, "MULTILINESTRING")
#cálculo de la distancia entre la costa y nuestros puntos
dist <- st_distance(iceland, grid)
#distancia con unidad en metros
head(dist[1,])## Units: [m]
## [1] 790.7906 1151.4360 1270.7603 3128.9057 2428.5677 4197.7472Visualizar la distancia calculada
Una vez obtenida la distancia para nuestros puntos, podemos combinarlos con las coordenadas y plotearlos en ggplot2. Para ello, creamos un data.frame. El objeto dist es una matriz de una columna, por eso, tenemos que convertirla a vector con la función as.vector( ). Además, dividimos por 1000 para convertir la distancia en metros a km. La función st_coordinates( ) extrae las coordenadas de nuestros puntos. Para la visualización usamos un vector de colores con la gama RdGy (más aquí).
#creamos un data.frame con la distancia y las coorendas de los puntos
df <- data.frame(dist = as.vector(dist)/1000,
st_coordinates(grid))
#estructura
str(df)## 'data.frame': 4104 obs. of 3 variables:
## $ dist: num 0.791 1.151 1.271 3.129 2.429 ...
## $ X : num 608796 613796 583796 588796 593796 ...
## $ Y : num 7033371 7033371 7038371 7038371 7038371 ...#colores
col_dist <- brewer.pal(11, "RdGy")
ggplot(df, aes(X, Y,fill = dist))+ #variables
geom_tile()+ #geometría
scale_fill_gradientn(colours = rev(col_dist))+ #colores para la distancia
labs(fill = "Distance (km)")+ #nombre de la leyenda
theme_void()+ #estilo del mapa
theme(legend.position = "bottom") #posición de la leyenda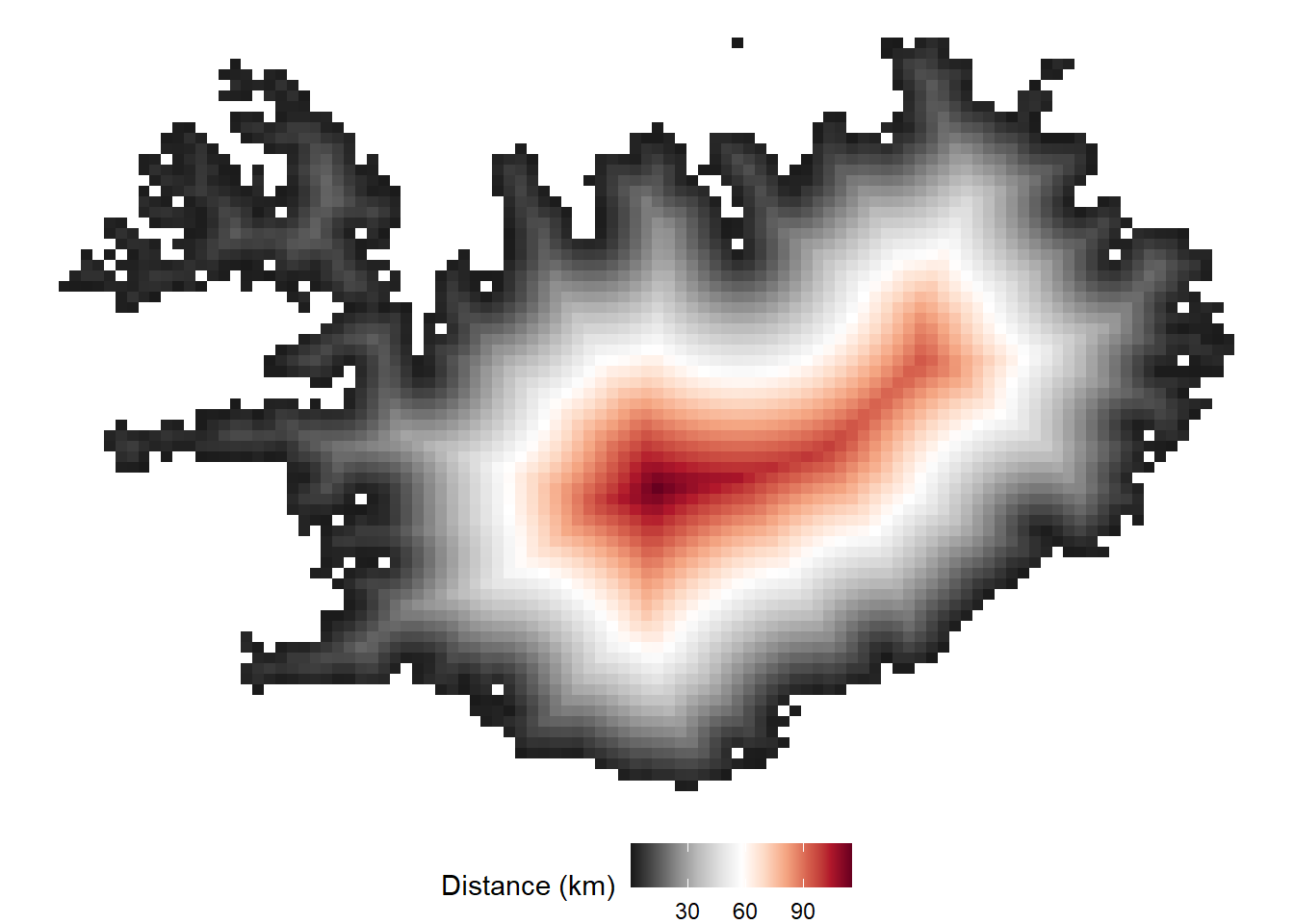
Exportar la distancia como raster
Para poder exportar la distancia con respecto al mar de Islandia, debemos usar la función rasterize( ) de la librería raster.
Primero, es necesario crear un raster vacío. En este raster debemos indicar la resolución, en nuestro caso es de 5000m, la proyección y la extensión del raster.
La proyección la podemos extraer de la información del mapa de Islandia.
La extensión la conseguimos extraer de nuestros puntos grid con la función
extent( ). No obstante, esta última función necesita la clase sp, por eso pasamos el objeto grid en formato sf, únicamente para ello, a la clase sp usando la funciónas( )y el argumento “Spatial”.
Además de lo anterior, el data.frame df que creamos antes debemos convertir en clase sf. Por eso, aplicamos la función
st_as_sf( )con el argumento coords indicando los nombres de las coordenadas. Adicionalmente, también definimos el sistema de coordenadas que conocemos.
#obtenemos la extensión
ext <- extent(as(grid, "Spatial"))
#objeto extent
ext## class : Extent
## xmin : 338795.6
## xmax : 848795.6
## ymin : 7033371
## ymax : 7383371#raster destino
r <- raster(resolution = 5000, ext = ext, crs = "+proj=utm +zone=27 +ellps=intl +towgs84=-73,47,-83,0,0,0,0 +units=m +no_defs")
#convertimos los puntos a un spatial object clase sf
dist_sf <- st_as_sf(df, coords = c("X","Y")) %>%
st_set_crs(3055)
#creamos el raster de la distancia
dist_raster <- rasterize(dist_sf, r, "dist", fun = mean)
#raster
dist_raster## class : RasterLayer
## dimensions : 70, 102, 7140 (nrow, ncol, ncell)
## resolution : 5000, 5000 (x, y)
## extent : 338795.6, 848795.6, 7033371, 7383371 (xmin, xmax, ymin, ymax)
## crs : +proj=utm +zone=27 +ellps=intl +units=m +no_defs
## source : memory
## names : layer
## values : 0.006124901, 115.1712 (min, max)#plotear el raster
plot(dist_raster)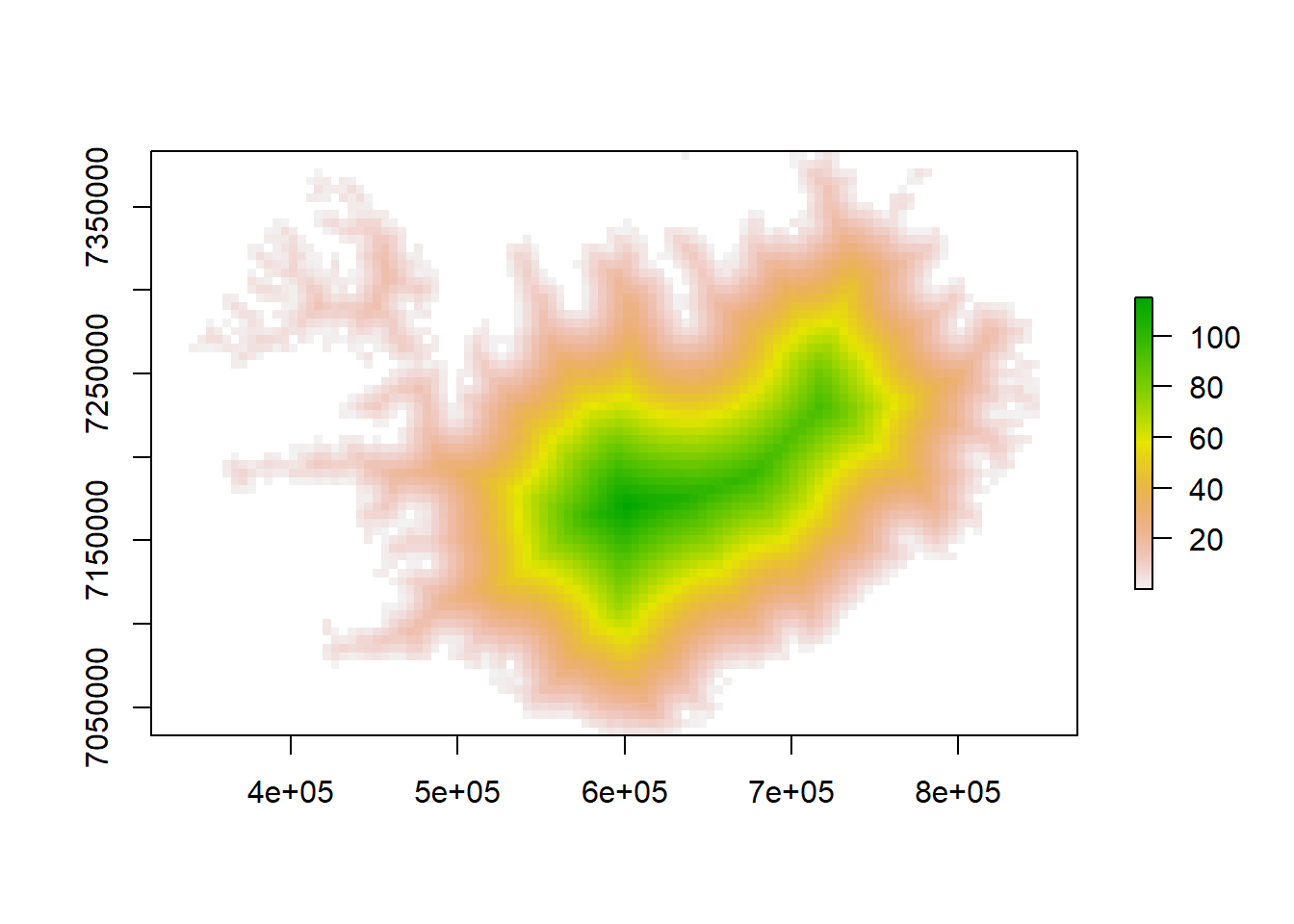
#exportamos el raster
writeRaster(dist_raster, file = "dist_islandia.tif", format = "GTiff", overwrite = TRUE)La función rasterize( ) está pensada para crear rasters a partir de un grid irregular. En caso que tengamos un grid regular, como este mismo, podemos usar una alternativa más fácil. La función rasterFromXYZ( ) convierte un data.frame con longitud, latitud y la variable Z en un raster. Es importante que el orden debe ser longitud, latitud, variables.
r <- rasterFromXYZ(df[, c(2:3, 1)], crs = "+proj=utm +zone=27 +ellps=intl +towgs84=-73,47,-83,0,0,0,0 +units=m +no_defs")
plot(r)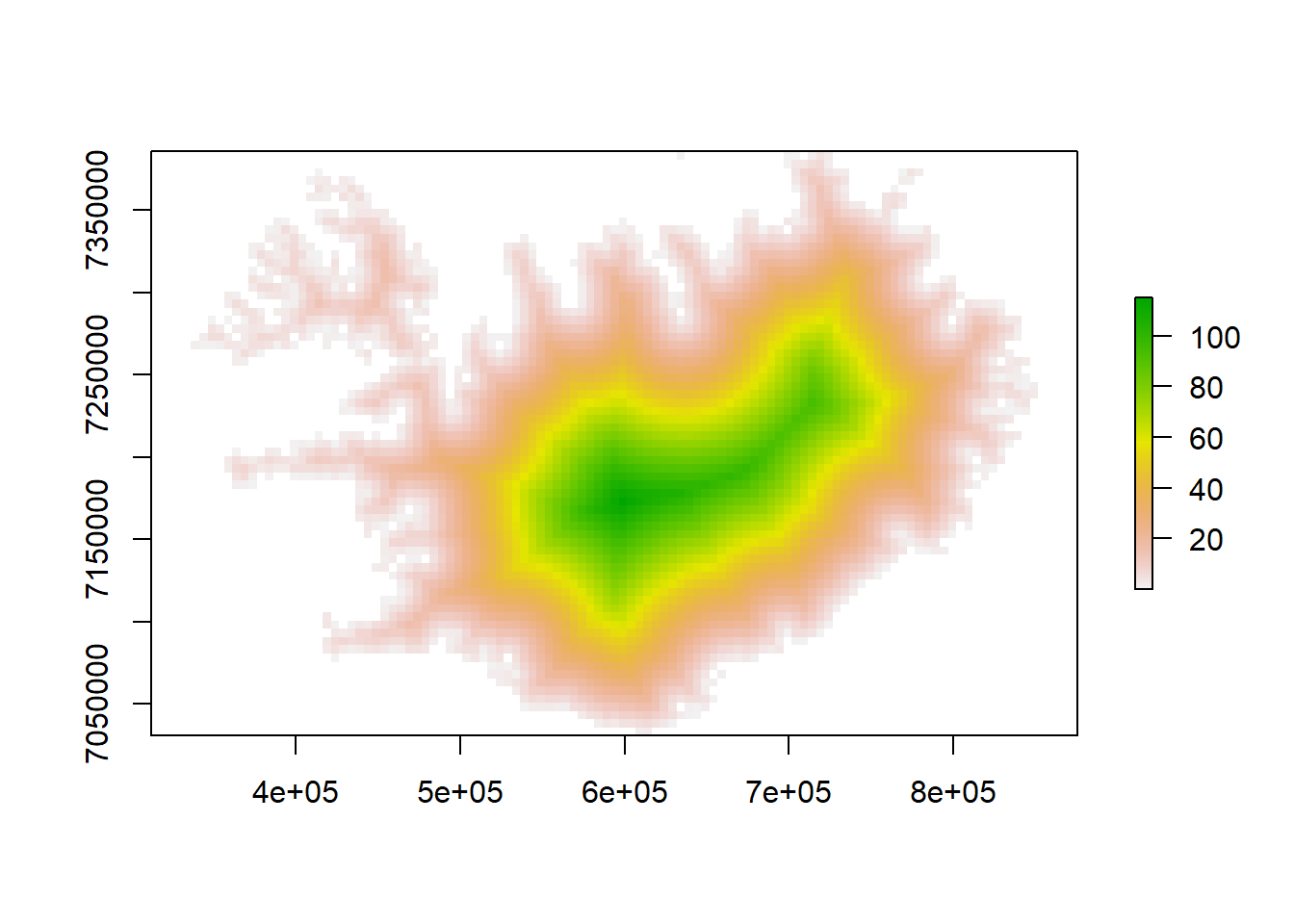
Con el cálculo de la distancia podemos llegar crear arte, como se ve en la cabezera de este post, que incluye un mapamundi únicamente con la distancia al mar de todos los continentes. Una perspectiva diferente a nuestro mundo (aquí más).