Mapa de círculos agrupados en múltiples localizaciones
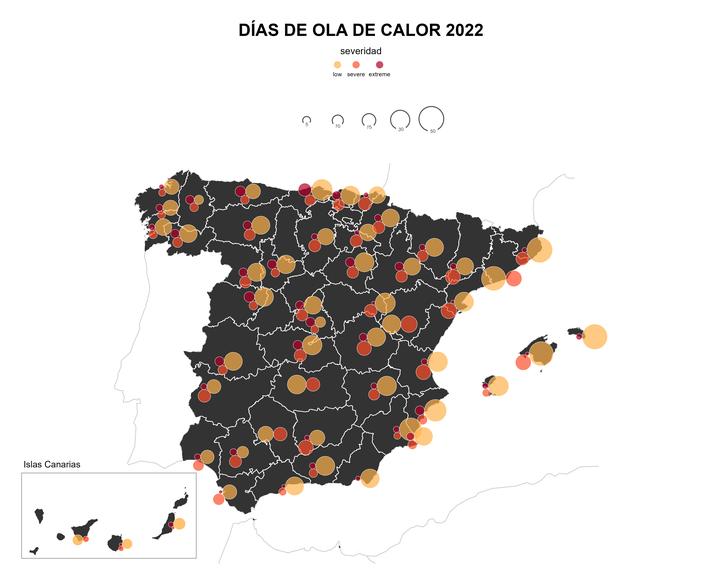
En mi primer post de 2024, que desgraciadamente no ha sido posible antes de abril, os voy a explicar como podemos agrupar en la misma localización varios círculos proporcionales. En 2022 estaba buscando cómo representar el número de días de olas de calor según el grado de gravedad en España. Encontré la solución usando el empaquetamiento de círculos que también se usa en el cartograma de Dorling.
Paquetes
| Paquete | Descripción |
|---|---|
| tidyverse | Conjunto de paquetes (visualización y manipulación de datos): ggplot2, dplyr, purrr,etc. |
| mapSpain | Límites administrativos de España a diferentes niveles |
| giscoR | Límites administrativos del mundo |
| sf | Simple Feature: importar, exportar y manipular datos vectoriales |
| ggtext | Mejorado soporte de renderizado de texto para ggplot2 |
| ggrepel | Proporciona geometrías ggplot2 para repeler etiquetas de texto superpuestas |
| geomtextpath | Añadir texto a líneas que puede seguir cualquier trayectoria y se mantendrá correctamente espaciado y angulado. |
| packcircles | Paquete R para el empaquetado de círculos. Algoritmos para encontrar círculos no superpuestos. |
| cartogram | Construye distinos tipos de cartogramas |
# instalamos los paquetes si hace falta
if(!require("tidyverse")) install.packages("tidyverse")
if(!require("mapSpain")) install.packages("mapSpain")
if(!require("sf")) install.packages("sf")
if(!require("packcircles")) install.packages("packcircles")
if(!require("ggtext")) install.packages("ggtext")
if(!require("ggrepel")) install.packages("ggrepel")
if(!require("cartogram")) install.packages("cartogram")
if(!require("giscoR")) install.packages("giscoR")
if(!require("rmapshaper")) install.packages("rmapshaper")
if(!require("geomtextpath")) install.packages("geomtextpath")
# paquetes
library(tidyverse)
library(lubridate)
library(sf)
library(mapSpain)
library(ggrepel)
library(ggtext)
library(packcircles)
library(cartogram)
library(giscoR)
library(rmapshaper)
library(geomtextpath)Datos
En este post usaremos los datos de las olas de calor registadas en el año 2022 (descarga). En su momento calculé el índice Excess Heat Factor para diferentes localidades de España. Podéis encontrar las formulas del cáclulo del índice en Díaz-Poso et al. (2023{:target=“_blank”}). Se trata de un geojson con el número de días de ola de calor según gravedad (low, severe, extreme) para 51 estaciones meteorológicas. Es necesario que los datos estén proyectados, en este caso es la ETRS89 UTM 30 (EPSG:25830). Además, importamos y modificamos los límites provinciales y globales para usarlos como base en el mapa.
# datos EHF olas de calor 2022
ehf <- st_read("ehf_2022_spain.geojson")## Reading layer `ehf_2022_spain' from data source
## `E:\GitHub\blog_update_2021\content\es\post\2024-04-20-mapa-empaquetamiento-circulos\ehf_2022_spain.geojson'
## using driver `GeoJSON'
## Simple feature collection with 148 features and 3 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -839774.5 ymin: 3150771 xmax: 1117513 ymax: 4815734
## Projected CRS: ETRS89 / UTM zone 30Nehf## Simple feature collection with 148 features and 3 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -839774.5 ymin: 3150771 xmax: 1117513 ymax: 4815734
## Projected CRS: ETRS89 / UTM zone 30N
## First 10 features:
## stat_name levels n geometry
## 1 BARCELONA AEROPUERTO low 48 POINT (924574.5 4583673)
## 2 BARCELONA AEROPUERTO severe 21 POINT (924574.5 4583673)
## 3 GIRONA AEROPUERTO extreme 2 POINT (978052.4 4656058)
## 4 GIRONA AEROPUERTO low 53 POINT (978052.4 4656058)
## 5 GIRONA AEROPUERTO severe 14 POINT (978052.4 4656058)
## 6 DONOSTIA / SAN SEBASTIÁN, IGELDO extreme 2 POINT (577768.2 4795286)
## 7 DONOSTIA / SAN SEBASTIÁN, IGELDO low 24 POINT (577768.2 4795286)
## 8 DONOSTIA / SAN SEBASTIÁN, IGELDO severe 14 POINT (577768.2 4795286)
## 9 BILBAO AEROPUERTO extreme 6 POINT (507593.1 4793918)
## 10 BILBAO AEROPUERTO low 31 POINT (507593.1 4793918)plot(ehf)
# límites provinciales España
esp <- esp_get_prov(moveCAN = FALSE, epsg = "4326")
plot(esp)
esp_pen <- filter(esp, nuts2.name != "Canarias")
# límites interiores de España
esp_inline <- rmapshaper::ms_innerlines(esp_pen)
# límites globales
eu <- gisco_get_countries(res = 10) |>
st_cast("MULTILINESTRING") |>
st_crop(xmin = -10, ymin = 34.7,
xmax = 4.4, ymax = 43.8)
plot(eu)
## canarias
canlim <- esp_get_ccaa("Canarias", moveCAN = FALSE)
bx <- st_bbox(canlim)Diagrama de Dorling
Cuando empecé a investigar posibilidades para lograr círculos en una posición agrupada sin sobrelapsarse, pensé directamente en la función cartogram_dorling() del paquete {cartogram}. El problema al que me enfrenté era que está diseñada para una única categoría, no obstante, como vemos tenemos hasta tres niveles de gravedad. Si usamos la función para la baja gravedad obtendremos el siguiente resultado.
# mapa Dorling de baja gravedad
dor <- cartogram_dorling(filter(ehf, levels == "low"), "n", k = .3)
# mapa
ggplot(dor,
aes(fill = n)) +
geom_sf(data = esp,
fill = "grey80",
colour = "white",
linewidth = .3) +
geom_sf() +
scale_fill_distiller(palette = "YlOrRd", direction = 1) +
labs(fill = NULL, title = "Número de días de calor de baja gravedad") +
theme_void() +
theme(legend.position = "top",
legend.key.height = unit(.5, "lines"),
legend.key.width = unit(3, "lines"),
plot.title = element_text(margin = margin(t = 5, b = 10), hjust = .5))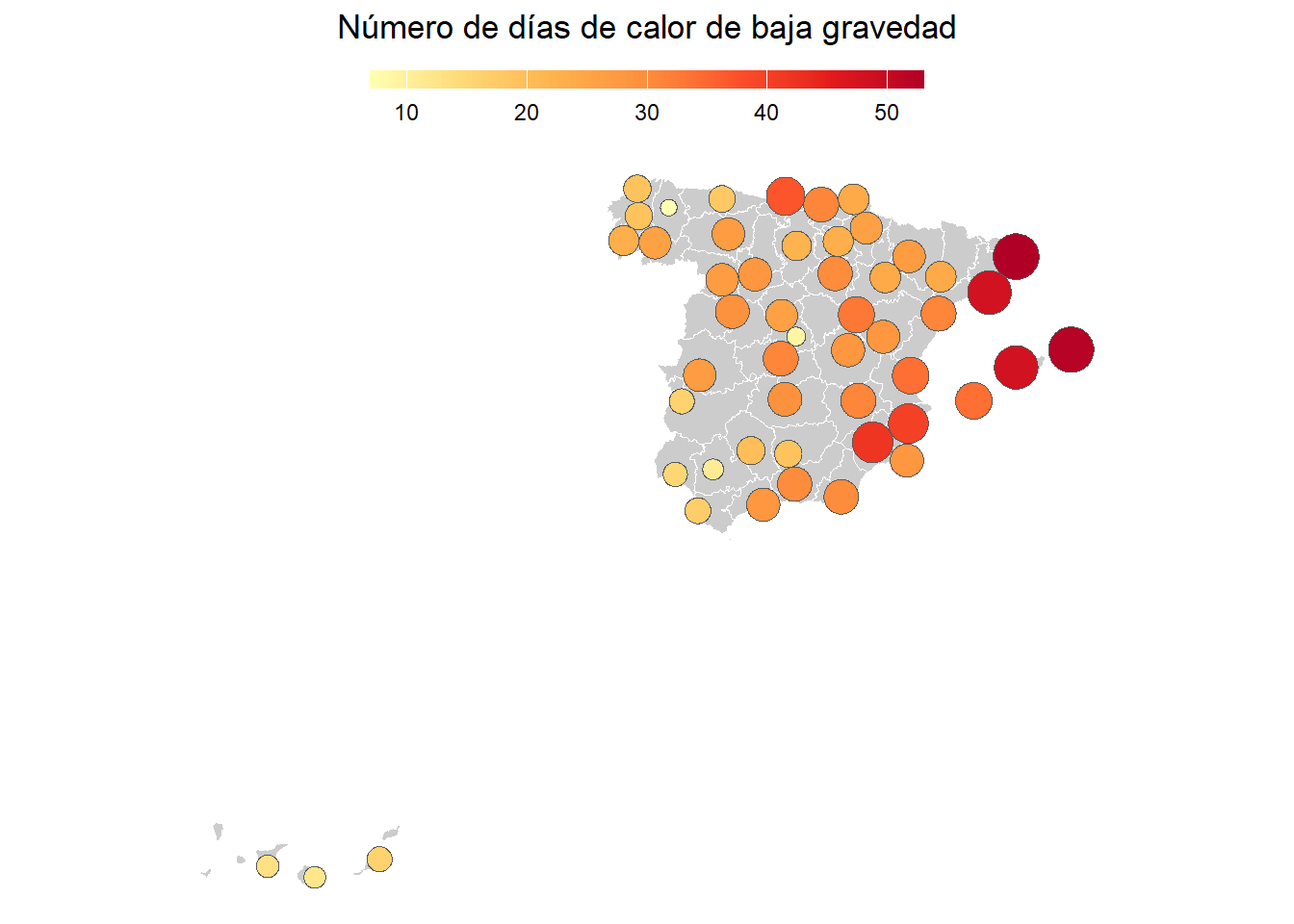
Pues bien, ¿qué podemos hacer? Debemos echar un vistazo más detallado a la función, la que nos facilita la creación del cartograma de Dorling (enlace). Primero podríamos crear un mapa de pequeños múltiples, pero un problema que encontramos es que no podemos fijar un valor máximo de una variable. Por eso, lo añadimos y modificamos ligeramente a la línea en la que se calcula el área (dat.init$v).
cartogram_dorling2.sf <- function(x, weight,
limit_mx = NULL, #new argument
k = 5,
m_weight = 1,
itermax= 1000){
# proj or unproj
if (sf::st_is_longlat(x)) {
stop('Using an unprojected map. This function does not give correct centroids and distances for longitude/latitude data:\nUse "st_transform()" to transform coordinates to another projection.', call. = F)
}
# no 0 values
x <- x[x[[weight]]>0,]
# data prep
dat.init <- data.frame(sf::st_coordinates(sf::st_centroid(sf::st_geometry(x))),
v = x[[weight]])
surf <- (max(dat.init[,1]) - min(dat.init[,1])) * (max(dat.init[,2]) - min(dat.init[,2]))
#dat.init$v <- dat.init$v * (surf * k / 100) / max(dat.init$v) # old
dat.init$v <- dat.init$v * (surf * k / 100) / ifelse(is_null(limit_mx),
max(dat.init$v),
limit_mx) # new argument
# circles layout and radiuses
res <- packcircles::circleRepelLayout(x = dat.init, xysizecols = 1:3,
wrap = FALSE, sizetype = "area",
maxiter = itermax, weights = m_weight)
# sf object creation
. <- sf::st_buffer(sf::st_as_sf(res$layout,
coords =c('x', 'y'),
crs = sf::st_crs(x)),
dist = res$layout$radius)
sf::st_geometry(x) <- sf::st_geometry(.)
return(x)
}Si ahora empleamos la función modificada, lograremos múltiples pequeños de Dorling. Simplemente debemos mapear la nueva función sobre cada categoría.
# estimamos el valor máximo
max_value <- max(ehf$n)
# mapeamos sobre cada categoría
dor2 <- split(ehf, ~ levels) |>
map(cartogram_dorling2.sf,
weight = "n",
k = .3,
limit_mx = max_value)
# reunimos las tablas y fijamos el orden
dor2 <- bind_rows(dor2) |>
mutate(levels = factor(levels, c("low", "severe", "extreme")))
# mapa de pequeños múltiples
ggplot(dor2,
aes(fill = n)) +
geom_sf(data = esp,
fill = "grey80",
colour = "white",
linewidth = .3) +
geom_sf() +
facet_grid(~levels) +
scale_fill_distiller(palette = "YlOrRd", direction = 1) +
labs(fill = NULL, title = "Número de días de calor de baja gravedad") +
theme_void() +
theme(legend.position = "top",
legend.key.height = unit(.5, "lines"),
legend.key.width = unit(3, "lines"),
plot.title = element_text(margin = margin(t = 5, b = 10), hjust = .5))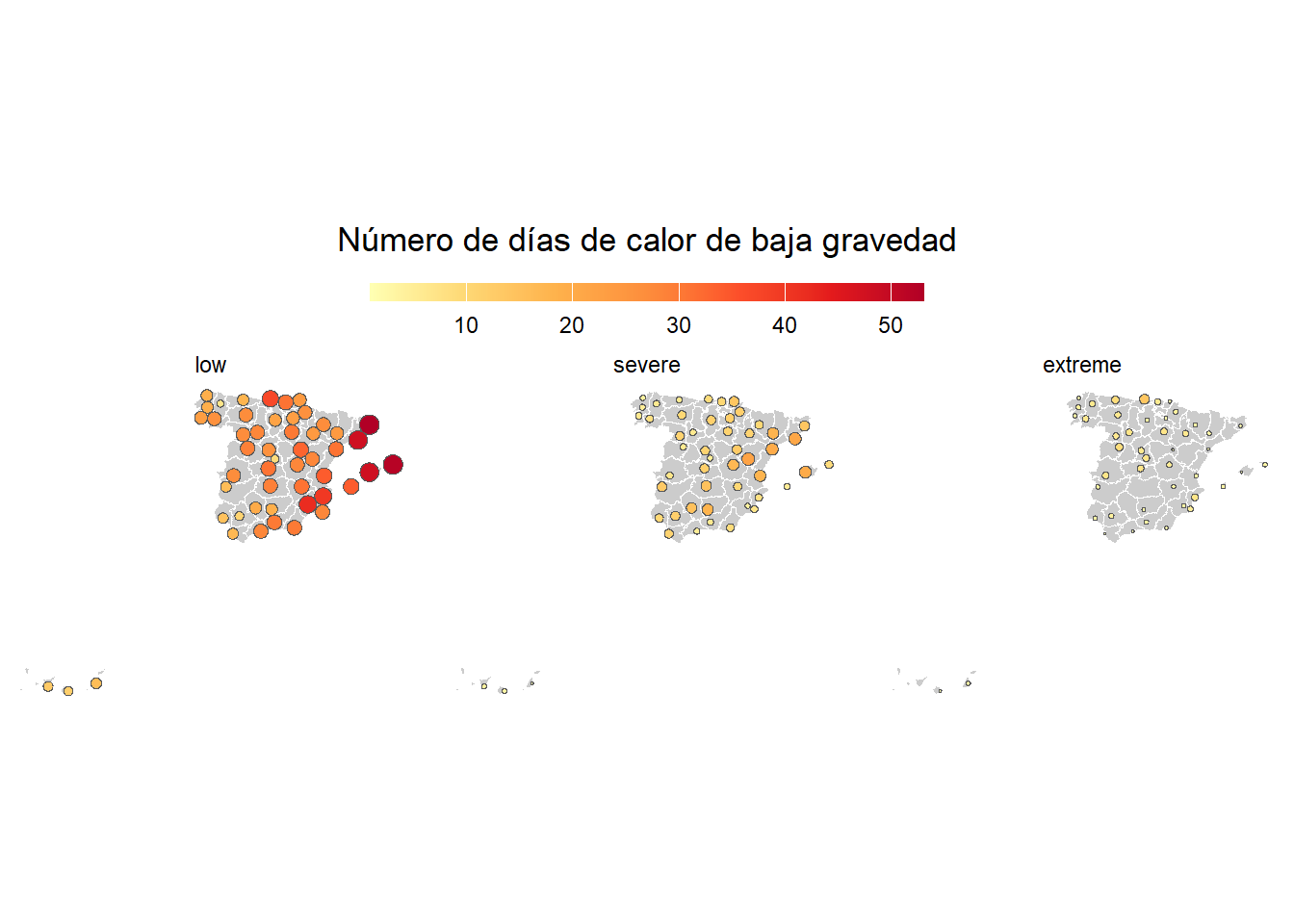
Me parecía interesante, pero no era lo que buscaba. También consideré hacer un mapa de símbolos proporcionales con círculos en la misma localización, empleando mezcla de color y transparencia al estilo de este mapa (enlace). Finalmente decidí modificar la función para lograr una posición agrupada con empaquetamiento de círculos. Introduje otro argumento surf = null para la extensión del conjunto de datos, además mantuve el cambio de introducir la posibilidad del valor máximo con el mismo objetivo, y cambié la función circleRepelLayout() a la circleProgressiveLayout(). La segunda ordena un conjunto de círculos, que se denotan por sus tamaños, colocando consecutivamente cada círculo externamente tangente a dos círculos colocados previamente evitando solapamientos. A diferencia del layout original en el que se ordenan los círculos mediante repulsión iterativa por pares dentro de un rectángulo delimitador. Otra alternativa potencial podría ser el uso de redes o grafos con {ggraph}, pero todavía no he llegado a probarlo.
packedcircle_dodge_position.sf <- function(x,
weight,
surf = NULL,
limit_mx = NULL, #new argument
k = .5){
# proj or unproj
if (sf::st_is_longlat(x)) {
stop('Using an unprojected map. This function does not give correct centroids and distances for longitude/latitude data:\nUse "st_transform()" to transform coordinates to another projection.', call. = F)
}
# no 0 values
x <- x[x[[weight]]>0,]
# data prep
dat.init <- data.frame(sf::st_coordinates(sf::st_centroid(sf::st_geometry(x))),
v = x[[weight]])
if(is_null(surf)) surf <- (max(dat.init[,1]) - min(dat.init[,1])) * (max(dat.init[,2]) - min(dat.init[,2]))
dat.init$v <- dat.init$v * (surf * k / 100) / ifelse(is_null(limit_mx),
max(dat.init$v),
limit_mx) # new argument
# circles layout and radiuses
res <- packcircles::circleProgressiveLayout(x = dat.init,
sizecol = "v") # other layout
res <- mutate(res, x = dat.init$X+x, y = dat.init$Y+y) # reconvert to lon, lat
# sf object creation
. <- sf::st_buffer(sf::st_as_sf(res,
coords =c('x', 'y'),
crs = sf::st_crs(x)),
dist = res$radius)
sf::st_geometry(x) <- sf::st_geometry(.)
return(x)
}Creación de círculos agrupados
Primero, debemos definir variables globales para todas las localizaciones. Entre otras, la extensión espacial de los datos, el valor máximo, el factor de escala para el tamaño, y la variable de interés.
limit_mx <- max(ehf$n) # valor máximo
longlat <- st_coordinates(ehf) # coordenadas en UTM
surf <- (max(longlat[,1]) - min(longlat[,1])) * (max(longlat[,2]) - min(longlat[,2])) # extensión
weight <- "n" # variable
k = .1 # factor de tamañoEn el siguiente paso, dividimos nuestros datos en tantos subconjuntos como localizaciones usando la función split(). Después aplicamos la función de agrupación a cada una de forma individual con map() pasando todos los argumentos globales previamente definidos. Después, solamente nos quedaría reunir todas las tablas espaciales.
# mapeamos sobre todas las localizaciones
circle_dodge <- split(ehf, ~ stat_name) |>
map(packedcircle_dodge_position.sf,
surf = surf, k = k,
weight = weight,
limit_mx = limit_mx)
# reunimos
circle_dodge <- bind_rows(circle_dodge) |>
mutate(levels = factor(levels,
c("low", "severe", "extreme"))) # fijamos orden
plot(circle_dodge["n"]) # resultado
Constucción del mapa
Leyenda
En la construcción del mapa lo primero que nos hace falta es la leyenda. Debemos crearla de forma manual definiendo diferentes magnitudes, en nuestro caso, número de días. A continuación estimamos el área y construimos los círculos de forma artificial en una línea constante de latitud en +45º, posición en la que insertaremos la leyenda como si fuese un objeto espacial.
# areas
legend_area <- c(5, 10, 15, 30, 50) * (surf * k / 100) / limit_mx
# construccion de circulos en coordenadas artificiales
legend_dat <- tibble(area = legend_area, r = sqrt(area/pi),
n = c(5, 10, 15, 30, 50), y = 45) |>
arrange(area) |>
mutate(x = -4:0) |>
st_as_sf(coords = c("x", "y"), crs = st_crs(esp)) |>
st_transform(25830) %>% # cambio al otro pipe para nested placehodler .
st_buffer(dist = .$r) |>
st_cast("LINESTRING")
plot(legend_dat["n"])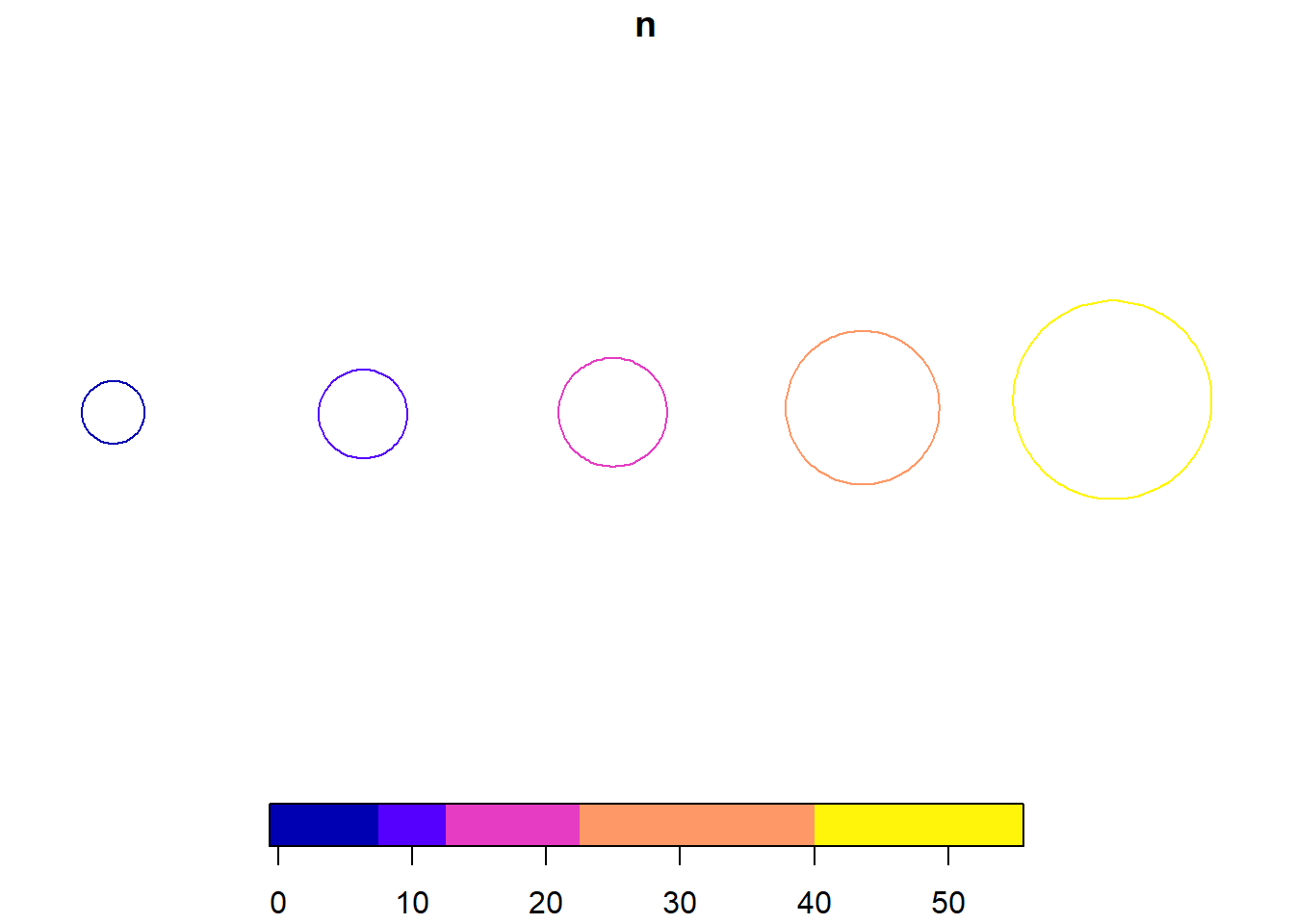
Una leyenda alternativa más compacta serían círculos colapsados, lo podremos lograr haciendo cambios en la posición con respecto al círculo más grande. No obstante, la leyenda en este caso queda pequeña por el maximo tamaño de los circulos. Un aumento del tamaño de los círculos llevaría a la sobreposición entre diferentes localizaciones.
# construccion de circulos en coordenadas artificiales
legend_dat2 <- tibble(area = legend_area, r = sqrt(area/pi),
n = c(5, 10, 15, 30, 50), y = 45) |>
arrange(area) |>
mutate(x = -3) |>
st_as_sf(coords = c("x", "y"), crs = st_crs(esp)) |>
st_transform(25830)
legend_dat2 <- cbind(legend_dat2, st_coordinates(legend_dat2)) |>
mutate(Y = Y-(max(r)-r)) |>
st_drop_geometry() |>
st_as_sf(coords = c("X", "Y"), crs = 25830) %>%
st_buffer(dist = .$r) |>
st_cast("LINESTRING")
plot(legend_dat2["n"])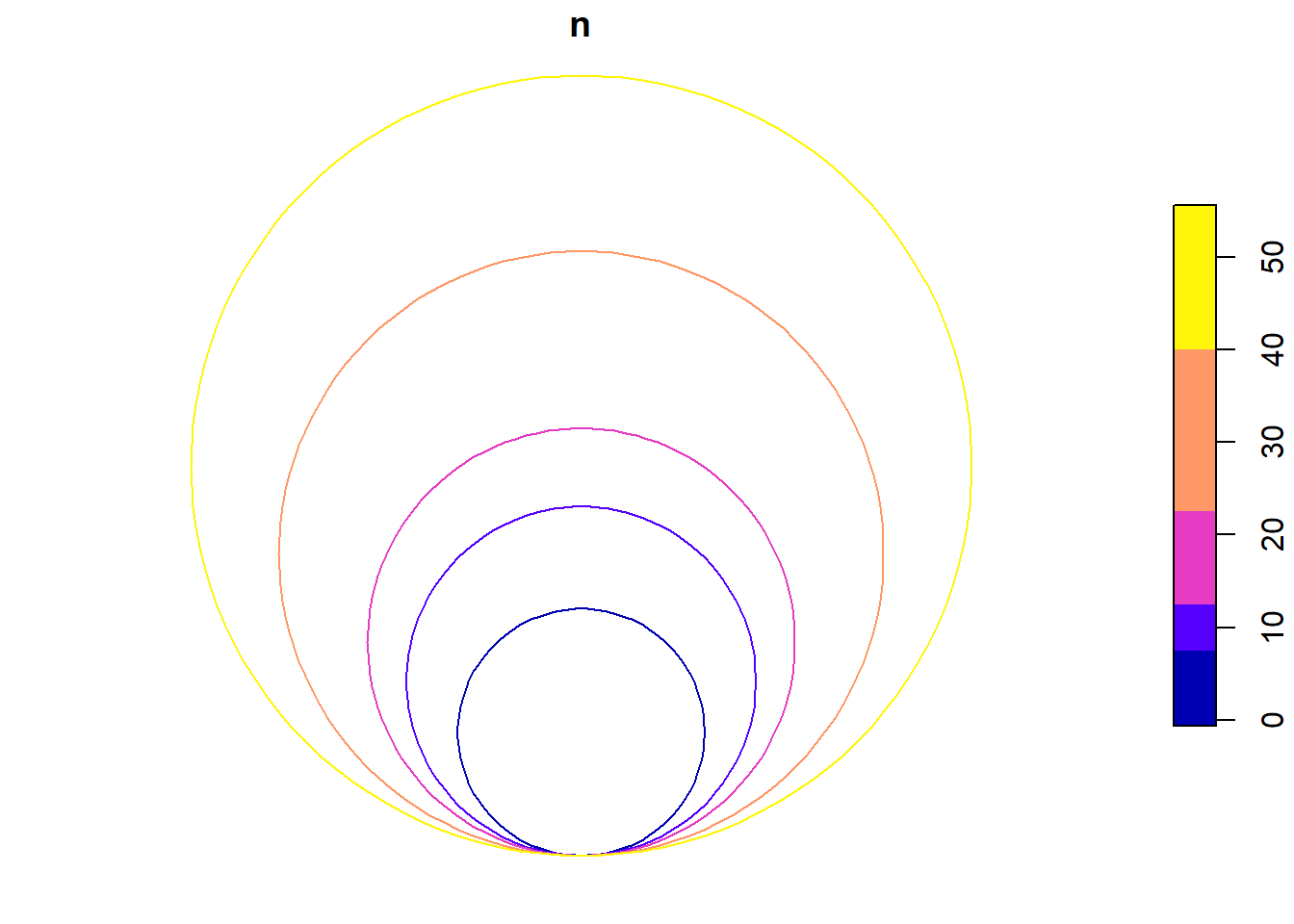
Canarias
El primer mapa correspondería a las Islas Canarias, el que se añade al mapa principal en una posición falsa. En ggplot2 cualquier geometría simple feature se puede añadir con geom_sf() ajustando las características propias de puntos, líneas o polígonos.
can <- ggplot() +
geom_sf(data = esp, fill = "grey20", colour = NA) +
geom_sf(data = esp_inline, colour = "white",
size = .2) +
geom_sf(data = circle_dodge,
aes(fill = levels),
alpha = .8,
colour = "white",
stroke = .025,
show.legend = FALSE) +
scale_fill_manual(values = c("#feb24c", "#fc4e2a", "#b10026"),
guide = "none") +
theme_void(base_family = "Lato") +
labs(title = "Islas Canarias") +
theme(plot.background = element_rect(fill = NA, colour = "black"),
plot.title = element_text(vjust = 8, margin = margin(b = 4, l = 3))) +
coord_sf(xlim = bx[c(1,3)],
ylim = bx[c(2,4)],
crs = 4326)
can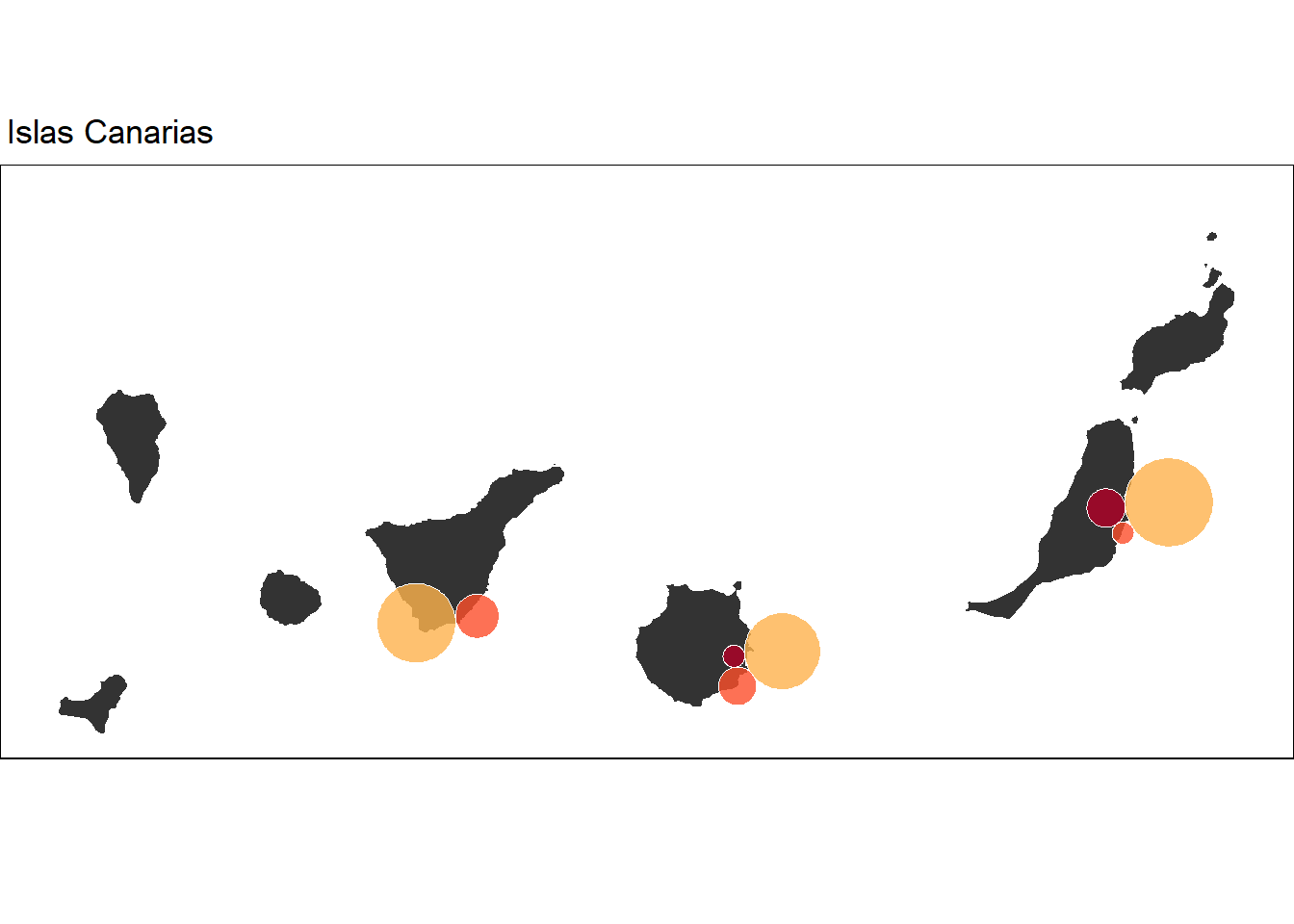
España
Para construir el mapa principal, excluiremos las localizaciones de las Islas Canarias. Además, necesitamos tener la nueva posición de las Islas Canarias en el suroeste de la Península. La diferencia principal con el mapa anterior es que incluimos la leyenda como objeto espacial usando la función geom_textsf(). Es una variante del paquete {geomtextpath} para añadir una etiqueta siguiendo cualquier trayectoria de la geometría. Desgraciadamente, no se pueden usar todos los argumentos posibles del paquete (issue). Es importante que la geometría es de tipo LINESTRING. Por eso, cambiamos el tipo con st_cast() anteriormente. Finalmente, insertamos el mapa mapa de Canarias empleando la función annotation_custom(). Más detalles sobre mapas insertado encontráis aquí.
# filtramos escacialmente únicamente localizaciones de España peninsular y Baleares
esp_data <- st_filter(circle_dodge, st_transform(esp_pen, 25830))
# coordenadas de la posición de Canarias
can_ext <- c(xmin = -11.74, ymin = 34.92, xmax = -7, ymax = 36.70)
class(can_ext) <- "bbox"
can_bbx <- st_as_sfc(can_ext) |>
st_set_crs(4326) |>
st_transform(25830) |>
st_bbox()
# primera parte añadiendo los limites base
g1 <- ggplot() +
geom_sf(data = eu, colour = "grey80", size = .3) +
geom_sf(data = esp_pen, fill = "grey20", colour = NA) +
geom_sf(data = esp_inline, colour = "white",
size = .2)
# añadimos los circulos proporacionales agrupados
g2 <- g1 + geom_sf(data = esp_data,
aes(fill = levels),
alpha = .7,
colour = "white",
stroke = .02,
show.legend = "point") +
geom_textsf(data = legend_dat, # leyenda en posicion artifical lat 45º
aes(label = n),
size = 2.5, hjust = .21) +
annotation_custom(ggplotGrob(can), # Islas Canarias
xmin = can_bbx[1], xmax = can_bbx[3],
ymin = can_bbx[2], ymax = can_bbx[4])
# ajustes finales de leyenda y estilo
g2 + scale_fill_manual(values = c("#feb24c", "#fc4e2a", "#b10026")) +
guides(fill = guide_legend(override.aes = list(size = 5, shape = 21))) +
labs(fill = "severidad", title = "DÍAS DE OLA DE CALOR 2022") +
theme_void() +
theme(legend.position = "top",
legend.text.position = "bottom",
legend.title.position = "top",
legend.text = element_text(vjust = 3),
legend.title = element_text(hjust = .5,
size = 14),
legend.margin = margin(t = 5),
plot.title = element_text(hjust = .5,
face = "bold",
size = 25,
margin = margin(b = 5, t = 20)),
plot.margin = margin(15, 2, 2, 5)) +
coord_sf(crs = 25830, clip = "off")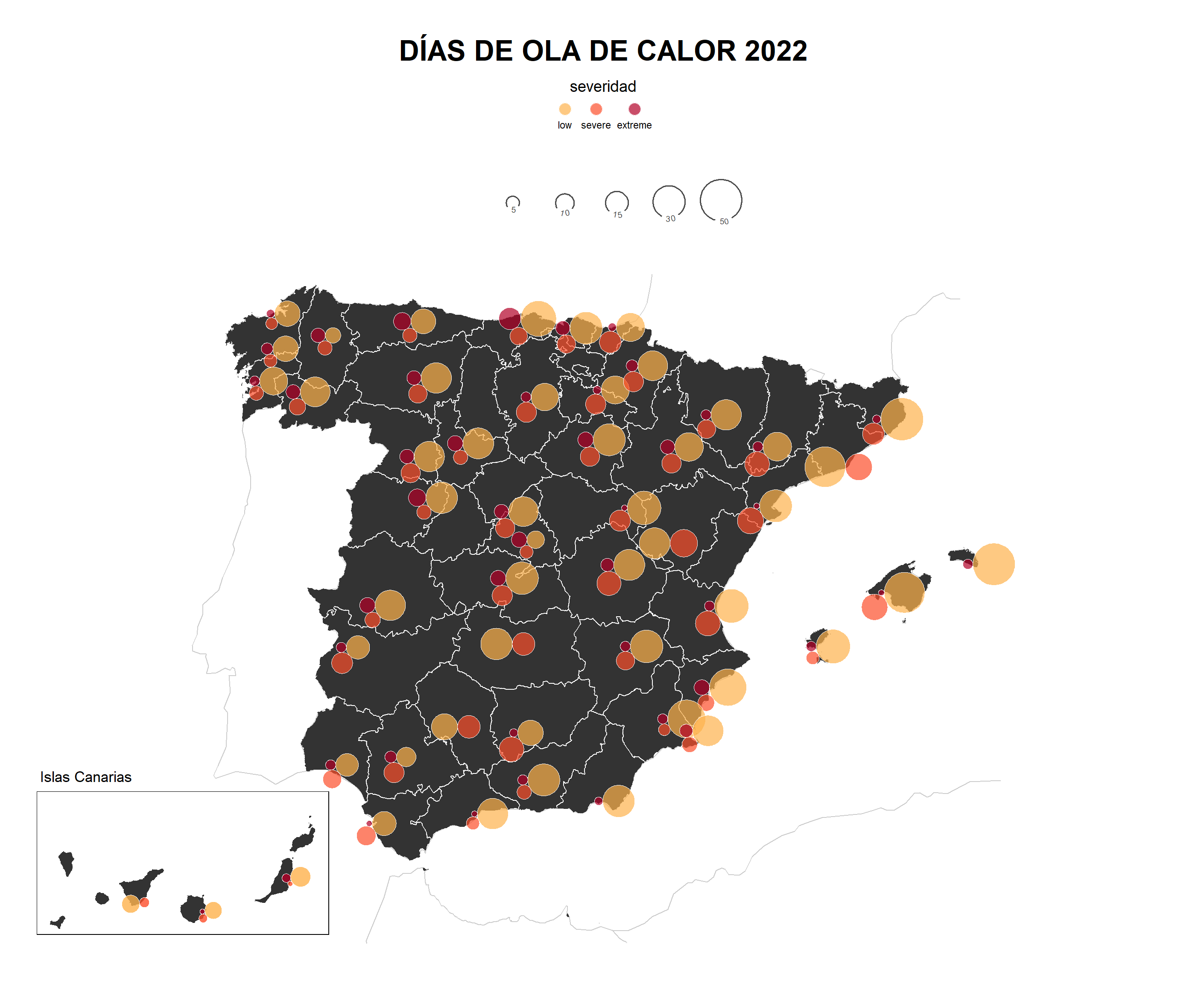
Versión interactiva
Como un extra de este post, aquí os muestro cómo podemos hacer el mismo mapa de forma interactiva usando el paquete {ggiraph}. Únicamente cambiamos la función geom_sf() por su variante geom_sf_interactivo(). Además, indicamos lo que queremos mostrar en el tooltip. Metemos el resultado en un objeto para finalizar de construir la versión interactiva empleando girafe() e incluyendo ajustes de estilo.
if(!require("ggiraph")) install.packages("ggiraph")
library(ggiraph) # versión interactiva de geometrias ggplot
# primera parte añadiendo los limites base
g1 <- ggplot() +
geom_sf(data = eu, colour = "grey80", size = .3) +
geom_sf(data = esp_pen, fill = "grey20", colour = NA) +
geom_sf(data = esp_inline, colour = "white",
size = .2)
# añadimos los circulos proporacionales agrupados
g2 <- g1 + geom_sf_interactive(data = esp_data,
aes(fill = levels, tooltip = n), # versión interactiva con tooltip
alpha = .7,
colour = "white",
stroke = .02,
show.legend = "point") +
geom_textsf(data = legend_dat,
aes(label = n),
size = 2.5, hjust = .21)
# ajustes finales de leyenda y estilo
g_final <- g2 + scale_fill_manual(values = c("#feb24c", "#fc4e2a", "#b10026")) +
guides(fill = guide_legend(override.aes = list(size = 5, shape = 21))) +
labs(fill = "severidad", title = "DÍAS DE OLA DE CALOR 2022") +
theme_void() +
theme(legend.position = "top",
legend.text.position = "bottom",
legend.title.position = "top",
legend.text = element_text(vjust = 3),
legend.title = element_text(hjust = .5,
size = 14),
legend.margin = margin(t = 5),
plot.title = element_text(hjust = .5,
face = "bold",
size = 25,
margin = margin(b = 5, t = 20)),
plot.margin = margin(15, 2, 2, 5)) +
coord_sf(crs = 25830, clip = "off")
# creación del mapa interactivo
girafe(ggobj = g_final,
width_svg = 14.69,
height_svg = 12,
options = list(
opts_tooltip(opacity = 0.7, use_fill = T)
))